What Are Quartiles? Statistics 101

In This Article

1. What Are Quartiles?

2. How Do Quartiles Work in Statistics?

3. Why Are Quartiles Important in Statistics?

4. How To Calculate Quartiles?

5. How To Interpret Quartiles?

6. Quartile Examples

What Are Quartiles?

In statistics, quartiles divide your data into four equal groups, each containing 25% (or a quarter) of your data points.

3 quartiles exist:

The First Quartile

The first quartile—also called the lower quartile or Q1—marks the 25th percentile of a data set. It divides the bottom quarter of your data from the second quarter.

The Second Quartile

The second quartile—also called the median or Q2—marks the 50th percentile of the data set. It divides the second quarter of your data from the third quarter. It also divides your data into two equal groups: the bottom 50 percent and the top 50 percent.

The Third Quartile

The third quartile—also called the upper quartile or Q3—marks the 75th percentile of the data set. It divides the third quarter of your data points from the top quarter.

How Do Quartiles Work in Statistics?

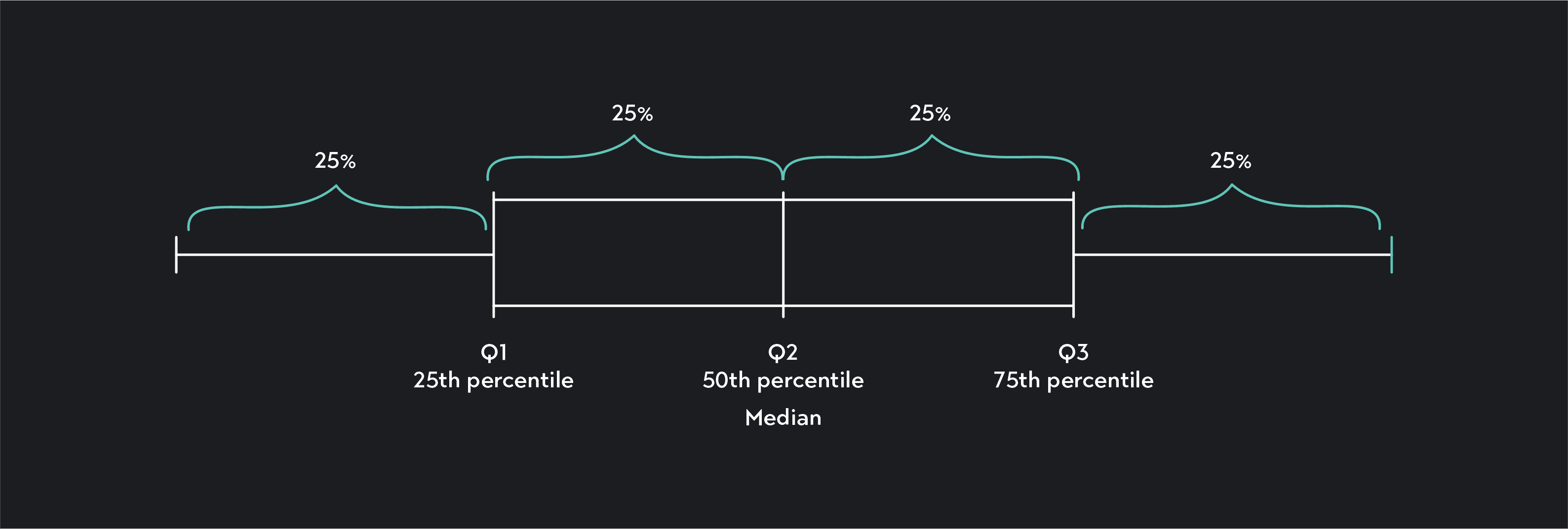
Quartiles are a type of quantile—a set of values that divide data into equal groups, each containing approximately the same number of observations.

Whenever you use quantiles, you arrange your data from smallest to largest, and the quantiles act as markers or cutoff points between each group.

Other commonly used quantiles include:

Percentiles

Percentiles divide data into 100 groups, each containing 1% of your observations.

Deciles

Deciles divide data into 10 groups, each containing 10% of your observations.

Quintiles

Quintiles divide data into 5 groups, each containing 20% of your observations.

Why Are Quartiles Important in Statistics?

Quartiles are useful because they provide a quick and easy way to summarize the spread and skewness of your data.

Once you know what your quartiles are, you can use them to contextualize other data points. For example, say you have data where Q1 is equal to 300, Q2 is equal to 500, and Q3 is 900. You can now take any data point, say 450, and know that it’s located between the 25th percentile and the median.

You can also use quartiles to construct the following related measures of location:

Five-Number Summary

The five-number summary is a list of the three quartiles and the minimum and maximum of your data.

Interquartile Range (IQR)

The interquartile range is the difference between the upper and lower quartiles (Q3-Q1). The IQR measures the dispersion of the middle 50 percent of your data.

Outliers

You can also use quartiles and the interquartile range to identify outliers in your data. The outlier formula describes any value greater than Q3 + (1.5 x IQR) and any value less than Q1 - (1.5 x IQR) as an outlier.

How To Calculate Quartiles?

Calculate Quartiles by Hand Using the Locator Method

To calculate quartiles by hand, follow these steps.

Step 1 - Count and Arrange Data Points

Count the number of data points and arrange them from smallest to largest. Arrange the data in ascending order and find the total $(n)$ number of values in your data.

Step 2 - Calculate Q1

To find Q1, multiply n by 25/100 (or ¼). This will give you a locator value, $L$.

If $L$ is a whole number, take the average of the $L^{th}$ value of the data set and the $(L+1)^{th}$ value. This average will be the first quartile.

If $L$ is not a whole number, round $L$ up to the nearest whole number and find the corresponding value in the data set. This will be the first quartile.

Step 3 - Calculate Q2 (The Median)

To find Q2, use the same method used to find Q1, except this time, multiply $n$ by 50/100 (or ½) to get the locator value, $L$.

Step 4 - Calculate Q3

To find Q3, use the same method used to find Q1, except this time, multiply $n$ by 75/100 (¾) to get the locator value, $L$.

Calculate Quartiles by Hand Using the Median Method

Another way of calculating quartiles by hand is by first identifying the median of the data. Here are the step-by-step instructions for calculating quartiles using the median method.

Step 1 - Find the median of the data (Q2)

To find the median (or Q2), arrange your data in ascending order. If the number of data points you have is odd, the median will be the middle value of your data. If you have an even number of data points, the median will be the average of the two middle numbers in your data.

Step 2 - Find the median of the lower half of the data

The median divides your set of data into two equal parts: a lower half and an upper half. You can calculate the first quartile (Q1), by finding the median of the lower half of the data.

Step 3 - Find the median of the upper half of the data

You can calculate the upper quartile (Q3) by finding the median of the upper half of your data.

Calculate Quartiles Using Excel or Google Sheets

To calculate quartiles in Excel or Google Sheets, use the QUARTILE() function. Because we can use different methods for calculating quartiles, the results you get from calculating quartiles in Excel or Google Sheets may be slightly different than the results you get when calculating quartiles by hand.

Step 1 - Find Q1

Suppose your data is in cells A1 through A20. To find Q1, type: =QUARTILE(A1:A20, 1)

Step 2 - Find Q2

To find Q2, use the same function, only this time, type a 2 before the closing parenthesis. Type =QUARTILE(A1:A20,2)

Step 3 - Find Q3

To find Q3, use the same function, but type a 3 before the closing parenthesis. Type =QUARTILE(A1:A20,3)

Calculate Quartiles Using R

To calculate quartiles in R, use the QUANTILE() function.

Suppose you have your data stored in a variable called $x$. You can find the three quartiles by typing: QUANTILE(x, probs = (0.25, 0.5, 0.75)).

You can also use the quantile function to find percentiles, deciles, and quintiles.

How To Interpret Quartiles?

Quartiles are ‌listed as a set of numbers or shown visually using a box plot or a box and whisker plot.

A box plot is a graph in the shape of a rectangle. The two shorter sides of the rectangle mark the lower and upper quartiles, and a line in the middle of the rectangle marks the median (Q2).

A box plot with two lines stretching out from either end of the rectangle is called a box and whisker plot. In addition to the three quartiles, a box and whisker plot marks the minimum and the maximum of your data.

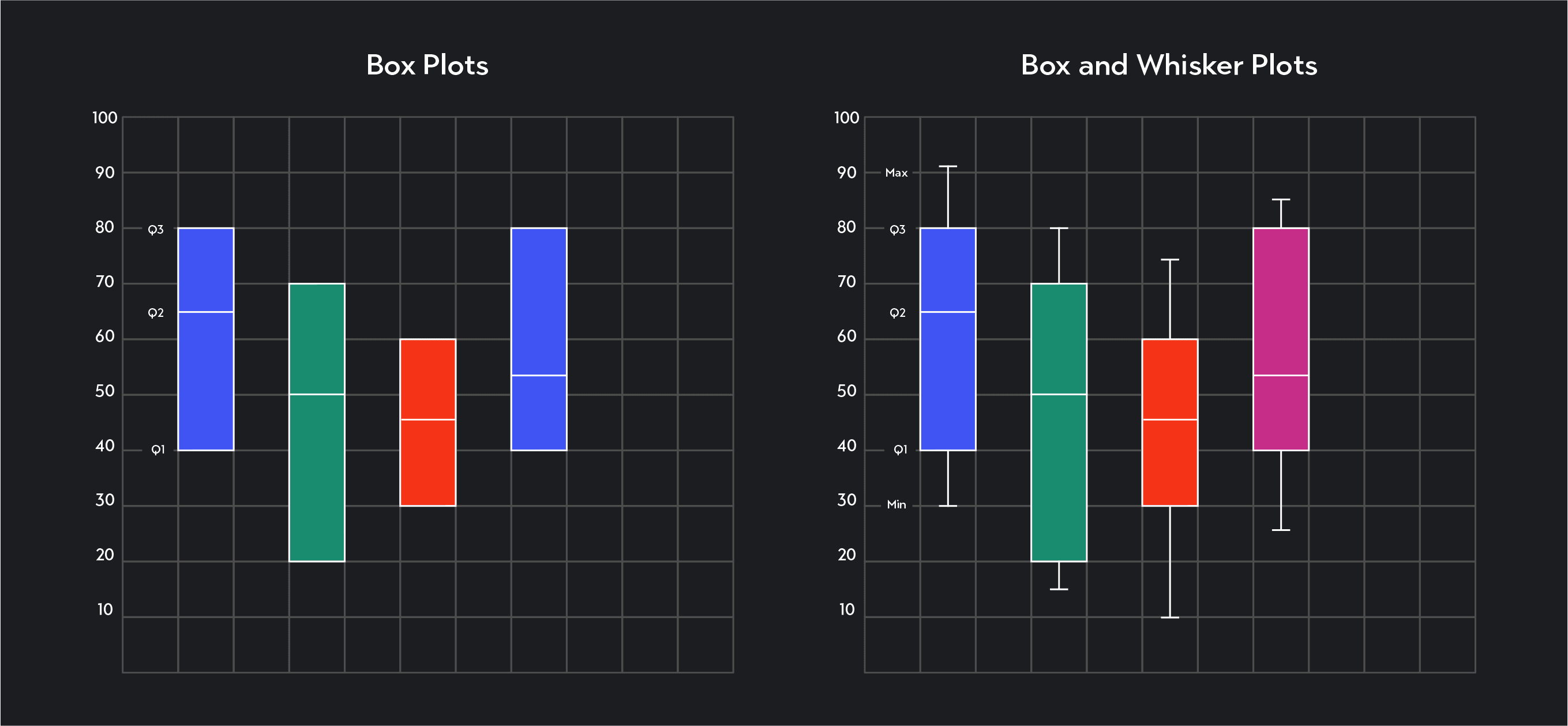
Whether you are looking at a list of quartiles, a boxplot, or a box and whisker plot, always remember what each quartile represents.

1. Q1 marks the 25th percentile of your data and divides the bottom quarter of your data from the second quarter.

2. Q2 marks the 50th percentile (the median) of your data and divides the second quarter of your data from the third quarter.

3. Q3 marks the 75th percentile of your data and divides the third quarter of your data points from the top quarter.

4. Subtracting Q3 from Q1 will give you the interquartile range (IQR). The IQR tells you how dispersed the middle 50 percent of your data is.

Quartile Examples

Here are two examples of quartiles calculated for different data sets. Notice that in each of these examples, we have already arranged the data in ascending order.

Example 1

*Answer will depend on what method you use

Example 2

*Answer will depend on what method you use

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Explore course

Intro to Statistics

How data describes our world.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course

Intro to Macroeconomics

How money moves our world.

Explore course

Intro to Macroeconomics

How money moves our world.

Explore course

Intro to Psychology

The science of the mind.

Explore course

Intro to Psychology

The science of the mind.

Explore course