What Do Subsets Mean in Statistics?

In This Article

1. What Is a Subset?

2. Types of Subsets

3. What Are the Subsets Symbols?

4. Subsets and Supersets

5. How Many Subsets Are in a Set?

6. What Is the Power Set of a Set?

7. Subset FAQs

Set theory is fundamental to mathematics. Mathematicians, statisticians, and data scientists use it, but can you? Of course. Anyone can learn the basics. Let’s explore how sets and subsets define, group, and organize mathematical objects.

What Is a Subset?

In statistics, a set is a collection of objects. The objects can be letters, numbers, shapes, symbols, or any other mathematical object. When we take a set apart, those smaller pieces are subsets.

A subset is a set made up of elements within another set. More formally, a set, B, is a subset of another set, A, if all elements in B are also in A.

Here are some examples:

• If Set A = {2, 4, 6, 8, 10} and Set B = {2, 6, 8}, Set B is a subset of Set A. All the elements in Set B are in Set A.

• If Set 1 = {a, b, c, d, e} and Set 2={a, b, c, z}, Set 2 is NOT a subset of Set 1. Although some elements of Set 2 are in Set 1, Set 2 also contains an element (the letter z) that is not in Set 1.

• If Set A is equal to the outcomes of a coin flip and Set B = {heads}, then Set B is a subset of Set A.

• If Set A is a set of whole numbers and Set B is a set of odd numbers, Set B is a subset of Set A.

• If Set 1 = {⚫, ⬛,⬟}, Set 1 is a subset of itself! This is true of all sets. We consider a set its own subset.

• If Set C = {1, 2, 3, 4, 5}, then the empty set, { }, is a subset of Set C. We always consider the empty set a subset of any set.

Types of Subsets

There are two types of subsets: proper subsets and improper subsets.

• A proper subset is any subset of a set, except the set itself.

• An improper subset is the set itself. We can also define an improper subset as any subset that is not a proper subset. The improper subset of Set A is Set A. Every set has only one improper subset.

Here’s another example.

Suppose Set A is a set consisting of all the letters in the English alphabet (26 letters). What are some of the proper subsets of Set A? What is the improper subset of Set A?

Set A has many proper subsets including {a,b,c, d}, {s, u, b}, {c, l, x, y, z}. Set A has only one improper subset—Set A!

What Are the Subsets Symbols?

We can use the symbol ⊂ or ⊆ to indicate a subset. ⊂ is the symbol used for proper subsets, and ⊆ is a symbol that can be applied for both proper and improper subsets.

The symbol ⊂ means “...is a proper subset of….”

The symbol ⊆ means “...is a proper or improper subset of...”

• B ⊂ A means that Set B is a proper subset of Set A. (Set B ≠ Set A)

• B ⊆ A means that Set B is either a proper or improper subset of Set A. (Set B may or may not be equal to Set A)

Subsets and Supersets

We can also describe subsets in terms of their supersets. If all the elements in Set B are in Set A, then Set A is called the superset of Set B. Said differently, if Set B is a subset of Set A, then Set A is a superset of Set B.

Supersets can also be proper or improper. A superset is an improper superset if it is the superset of itself—Set A is the improper superset of Set A. If a superset is not an improper superset, it is a proper superset.

The symbols used for supersets are ⊃ and ⊇. These symbols are the mirror image of the symbols used for subsets.

• A ⊃ B means that Set A is a proper superset of Set B. (Set A ≠ Set B)

• A ⊇ B means that Set A is either a proper or improper superset of Set B. (Set A may or may not be equal to Set A).

How Many Subsets Are in a Set?

Every set has $2^n$ subsets and $2^n-1$ proper subsets, where n is the number of elements in the set. You can check this formula with any set that comes to mind.

As an example, take the set {a, b, c}. This set has three elements, so n=3, and the total number of subsets is $2^3 = 8$. This set will have 7 proper subsets and 1 improper subset.

Notice that the last subset in the list is the empty set { }. An empty set is a set with no elements in it. It is sometimes called the null set and its symbol is ∅. We consider the empty set a subset of every set!

What Is the Power Set of a Set?

A power set is a set containing all subsets of a set. P( ) is its symbol.

It’s important to note that the power set is not the same thing as the superset.

If Set A = {a, b, c}, the power set, P(A) is a set with 2^n<\katex> elements.

The superset of A could be {a, b, c, d, e} or any other set containing the elements a, b, and c.

See if you can construct the power set for a set containing the outcomes of a coin toss!

You should get the power set { {heads, tails}, {heads}, {tails}, { } }

Subset FAQs

What Is the Definition of Subset?

A set, B, is a subset of another set, A if all elements in B are also in A.

What Is Set Theory?

Set theory is a branch of math that studies the logic and relationships between sets. A set is any collection of mathematical objects. To learn more about sets, read about set operations.

Can a Set Be a Subset of Itself?

Yes! A set is always a subset of itself. When you want to refer to a set as the subset of the set itself, you use the term improper subset.

Is the Null or Empty Set Considered a Subset?

Yes! We consider the null (or empty) set { } a subset of every set.

How Can You Figure Out How Many Subsets a Set Has?

A set always has $2^n$ subsets, where n is the number of elements in the original set. For example, a set containing 5 elements will have $2^5$ = 32 subsets.

How Many Subsets Does the Null Set Have?

The null set has 0 elements in it, so it will have $2^0$ subsets. $2^0 = 1$.

What Are Some Examples of Subsets?

Subsets, like sets, can consist of:

• Numbers

• Letters

• Shapes

• Symbols

• Points in space

• Any other mathematical object

A subset can even contain other sets!

Here are a few examples:

• The set {1, 3, 5} is a subset of {1, 3, 5, 8, 9}

• The set {like, disklike} is a subset of the set {like, dislike, no preference}

• A set of even numbers is a subset of set of whole numbers

• The set of natural numbers is a subset of real numbers

• The set {⚫} is a subset of {⚫, ⬛,⬟}

How Do You Represent a Subset in a Venn Diagram?

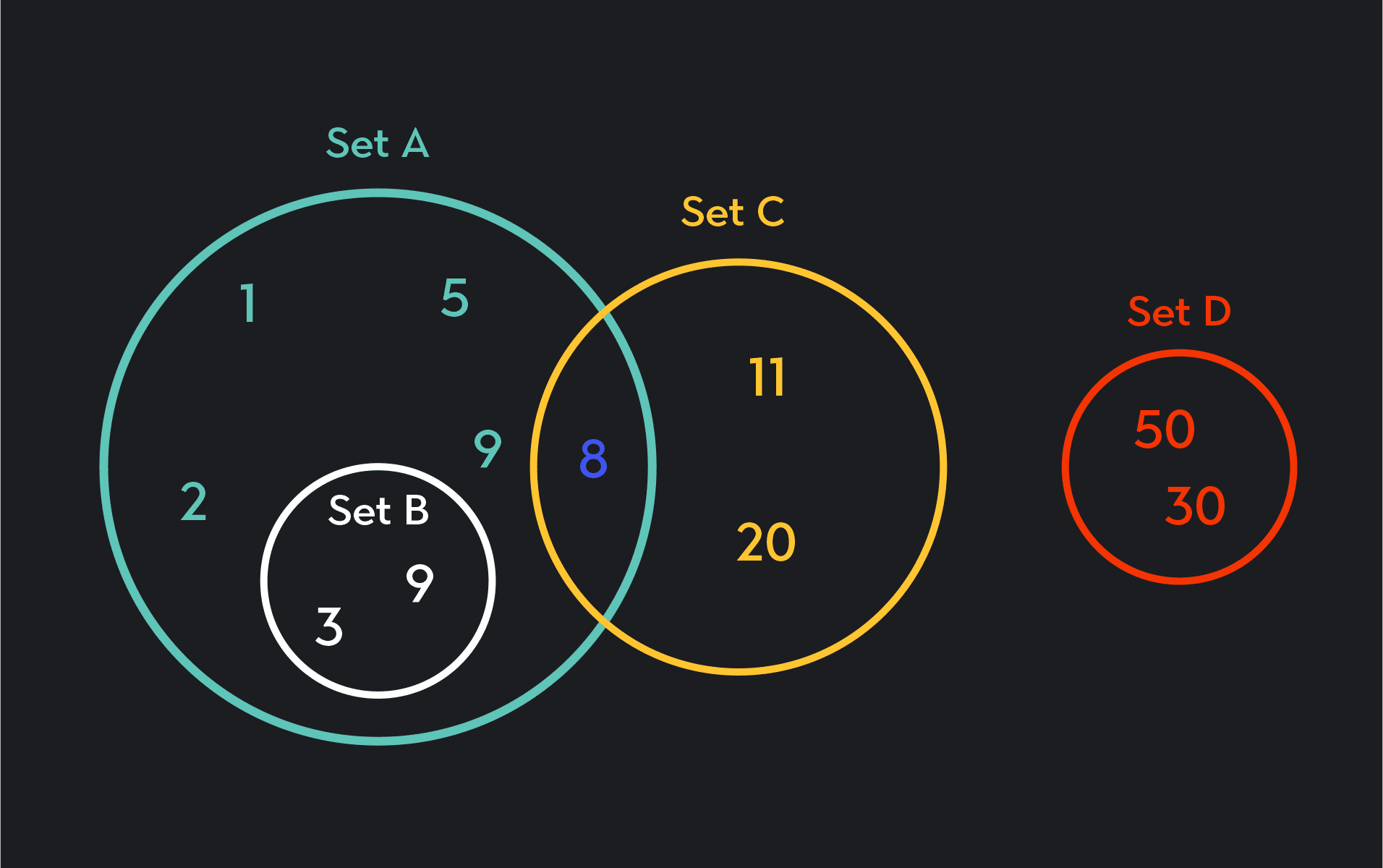
Venn diagrams are visual representations of sets. Because a subset c, you can represent a subset as a circle drawn within the boundaries of a larger circle representing the superset.

In the figure below, Set B is a subset of Set A.

• Set A = {1, 2, 3, 5, 7, 8, 9}

• Set B= {8}

• Set C = {8, 11, 20}

• Set D={30, 50}

Now that you know what a subset is, you can dive more into concepts like set operations and set notation. There’s even a first ever set theory clock in Berlin called the Mengenlehreuhr. It tells the time with illuminated, colored fields instead of numbers. How will you explore and expand your knowledge next?

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Explore course

Intro to Statistics

How data describes our world.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course

Intro to Macroeconomics

How money moves our world.

Explore course

Intro to Macroeconomics

How money moves our world.

Explore course

Intro to Psychology

The science of the mind.

Explore course

Intro to Psychology

The science of the mind.

Explore course