Statistics
What Do Subsets Mean in Statistics?
This article explains what subsets are in statistics and why they are important. You’ll learn about different types of subsets with formulas and examples for each.
Sarah Thomas
Subject Matter Expert
Outlier Articles Home
Statistics
Discrete vs. Continuous Variables: Differences Explained
02.17.2022 • 4 min read
Sarah Thomas
Subject Matter Expert
This article explains the concept of discrete, continuous, and random variables. You’ll also learn the differences between discrete and continuous variables.
In This Article
Don't Overpay For College Statistics
Take Intro to Statistics Online with Outlier.org
From the co-founder of MasterClass, earn transferable college credits from the University of Pittsburgh (a top 50 global school). The world's best online college courses for 50% less than a traditional college.
Get started
What Is a Variable?
To understand what discrete, continuous, and random variables are, you first need to know what a variable is.
In math, a variable is a quantity that can take on different values. It is a quantity that “varies.”
We typically denote variables using a lower-case or uppercase letter of the Latin alphabet, such as , , , or . You can attach a subscript to the letter to provide more information about the variable. For example, if is a variable representing height, you might use h1 and h2 to differentiate between the height of two different people. Similarly, you could write and to differentiate between a variable that represents the heights of males and the heights of females.
Categorical Variables and Numerical Variables
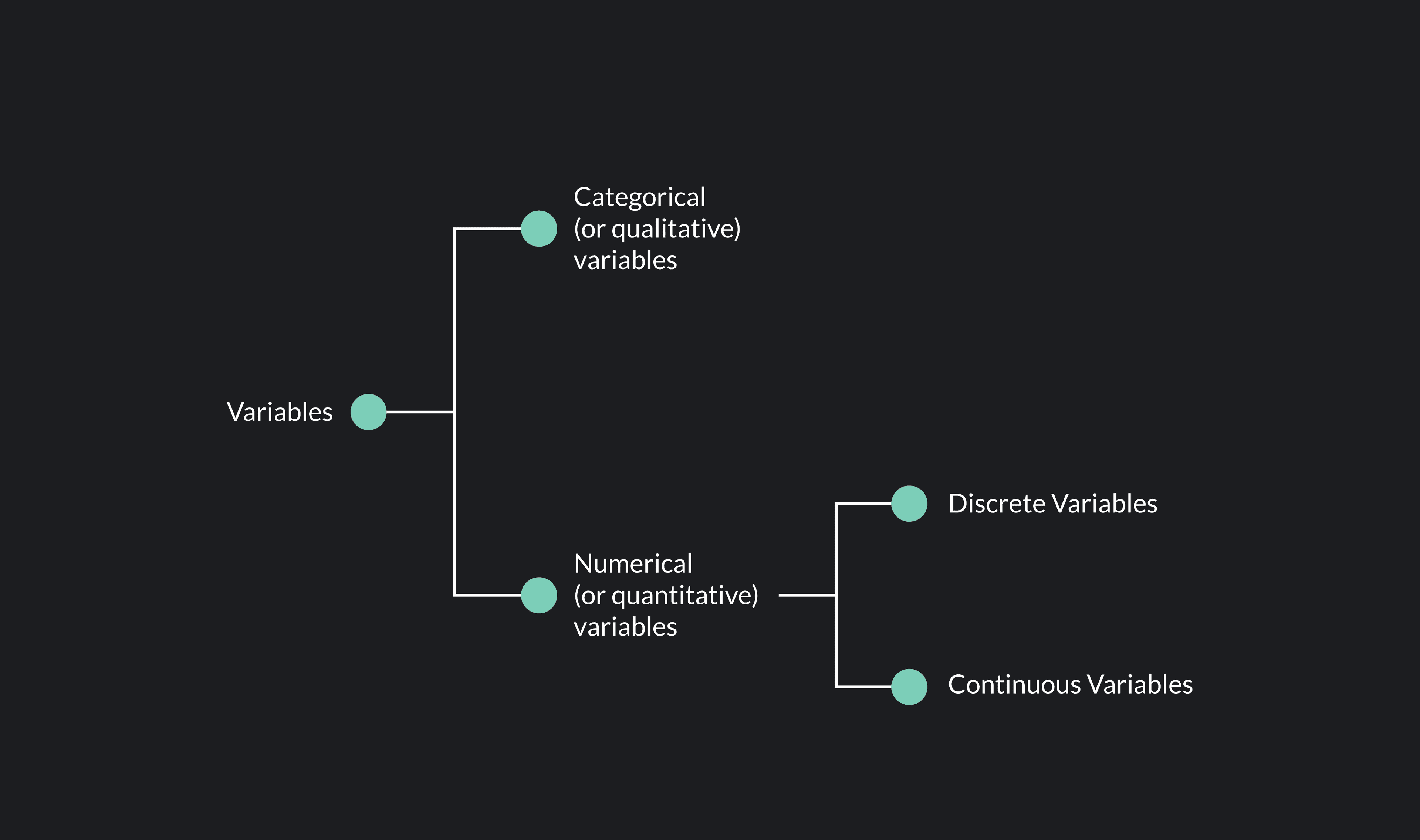
Variables can be categorical or numerical.
Categorical—also called qualitative—variables consist of names and labels that divide data into specific categories. When you select your nationality or your race on a survey, those responses are categorical.
Numerical—also called quantitative—variables have values that can either be counted or measured. Discrete and continuous variables are specific types of numerical data.
Main Characteristics of Discrete Data
Now that you know what a discrete random variable is, you may be wondering: Is there a difference between the terms “discrete variable” and “discrete data”?
In statistics and data analysis, a variable is any characteristic or attribute that can be measured. Data refers to the values or observations that are collected for a particular variable. For example, if you have a discrete random variable representing years of schooling, the data you collect would be discrete data.
Discrete data has the following main characteristics:
The data is collected for one or more discrete random variables
The observations in your data are limited in number
The observations in your data are countable and indivisible
A data set that consists only of data collected for discrete variables is called a discrete data set.
What Is a Continuous Variable?
A continuous variable is a variable that can take on any value within a range. A continuous variable takes on an infinite number of possible values within a given range.
Because the possible values for a continuous variable are infinite, we measure continuous variables (rather than count), often using a measuring device like a ruler or stopwatch. Continuous variables include all the fractional or decimal values within a range.
Examples
Examples of continuous variables include:
The time it takes sprinters to run 100 meters
The size of real estate lots in a city
The weight of baby elephants
The body temperature of patients with the flu
The deployment altitude of skydivers
None of these variables are countable. This is the key difference between discrete and continuous variables. A continuous variable can take on an infinite number of values within a range.
Main Characteristics of Continuous Data
What is continuous data? Continuous data are observations or data points collected for a continuous random variable. Let’s say you’re interested in the time it takes 5th graders to run a 50-yard dash.
This is a continuous random variable. Now, if you go out and collect a sample of 100 5th graders and record the time it takes each of them to run the dash, you’ll have a continuous data set consisting of 100 data points.
Continuous data has the following main characteristics:
The data is collected for one or more continuous random variables
The observations in your data could take on an infinite number of possible values within a range
The data are measured rather than counted
Are Continuous Variables Treated as Discrete Variables?
Sometimes we treat continuous variables as if they were discrete.
Age is an excellent example of this. If you know a person’s time of birth, you could measure their age precisely up to the second or even millisecond if you wanted to. In this sense, age is a continuous variable. However, we don’t usually care about a person’s exact age. Instead, we treat age as a discrete variable and count age in years.
What Is a Random Variable?
A random variable is a variable where the values are the outcome of a random process.
An easy example of a random variable is:
When you roll a die, the roll itself is a random event. The possible values of X are 1, 2, 3, 4, 5, or 6, but the specific value you get depends on the randomness of the event. It’s uncertain which number will appear on any given roll. You can learn more about events and the odds of of results when you read our article about math probability.
Random variables can be numerical or categorical, continuous or discrete.
Main Differences Between Discrete and Continuous Variables
The table below summarizes the key differences between discrete and continuous variables with examples.
| DISCRETE VARIABLES | CONTINUOUS VARIABLES |
| Definition- A discrete variable is a variable that takes on distinct, countable values. | Definition- A continuous variable is a variable that takes on any value within a range, and the number of possible values within that range is infinite. |
| Discrete variables have values that are counted. | The values of a continuous variable are measured. |
Discrete Variable Examples
| Continuous Variable Examples
|
Key Differences: Continuous vs. Discrete Data
The main difference between discrete data and continuous data is that discrete data is data collected for a discrete random variable, while continuous data is data collected for a continuous random variable.
Explore Outlier's Award-Winning For-Credit Courses
Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.
Check out these related courses:
Related Articles
Statistics
Set Operations: Formulas, Properties, Examples & Exercises
Here is an overview of set operations, what they are, properties, examples, and exercises.
Sarah Thomas
Subject Matter Expert
Calculus
Definite Integrals: What Are They and How to Calculate Them
Knowing how to find definite integrals is an essential skill in calculus. In this article, we’ll learn the definition of definite integrals, how to evaluate definite integrals, and practice with some examples.
Rachel McLean
Subject Matter Expert
Further Reading
Understanding Math Probability - Definition, Formula & How To Find It
Set Operations: Formulas, Properties, Examples & Exercises
Calculate Outlier Formula: A Step-By-Step Guide
Z-Score: Formula, Examples & How to Interpret It
A Step-by-Step Guide on How to Calculate Standard Deviation
Mean Absolute Deviation (MAD) - Meaning & Formula