Statistics
What Is Set Notation? [+ Bonus Practice]
Learn what a set notation is and why it is important. Create a set notation with the right structure and get reading and writing practice.
Sarah Thomas
Subject Matter Expert
Outlier Articles Home
Statistics
Set Operations: Formulas, Properties, Examples & Exercises
01.21.2022 • 6 min read
Sarah Thomas
Subject Matter Expert
Here is an overview of set operations, what they are, properties, examples, and exercises.
In This Article
What Are Set Operations?
Set operations describe the relationship between two or more sets. In math, a set is just a collection of objects.
These objects (more commonly referred to as elements) can take many forms, such as:
Numbers
Letters
Variables
Points
Shapes
Symbols
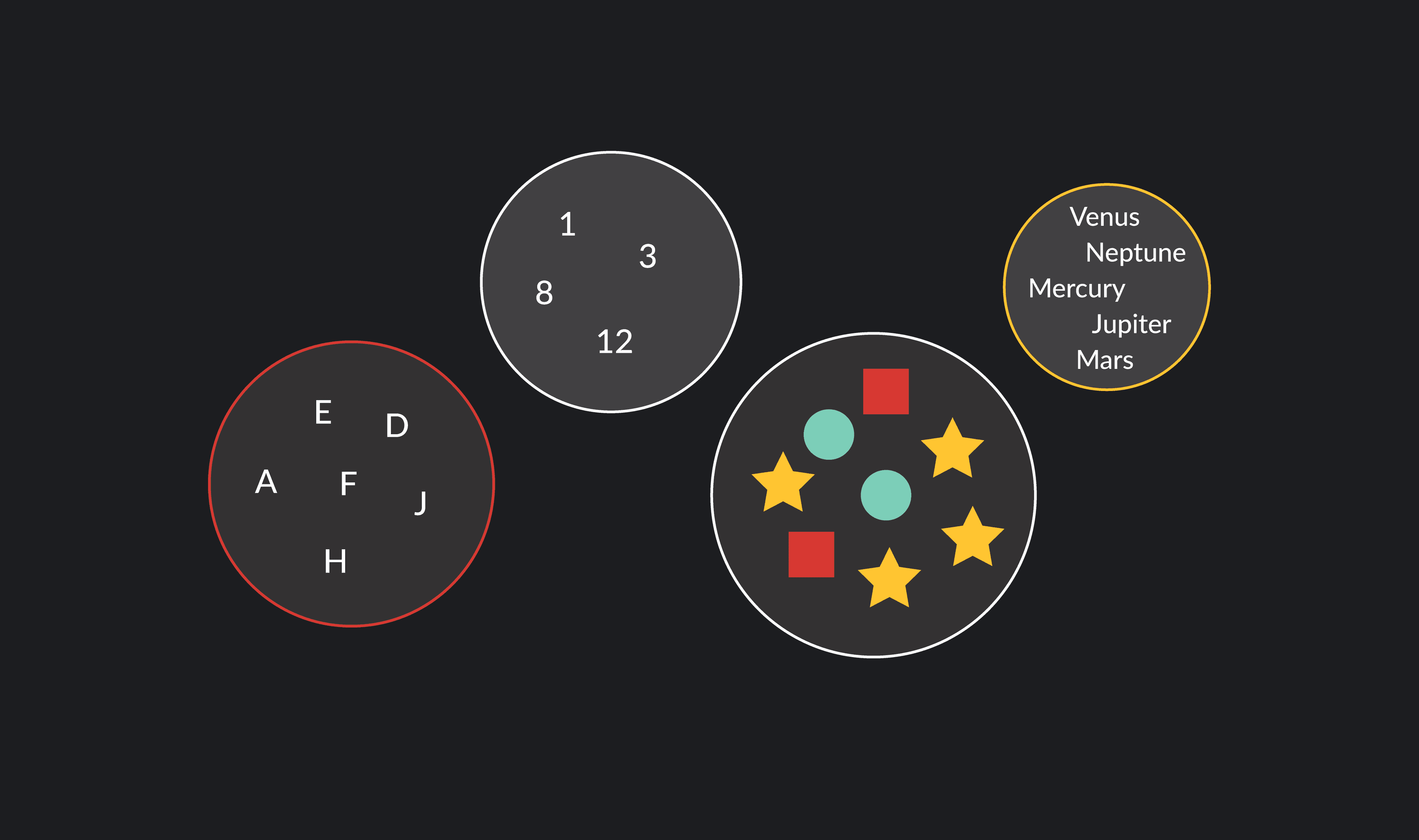
The most common set operations are:
Set Operations and Venn Diagrams
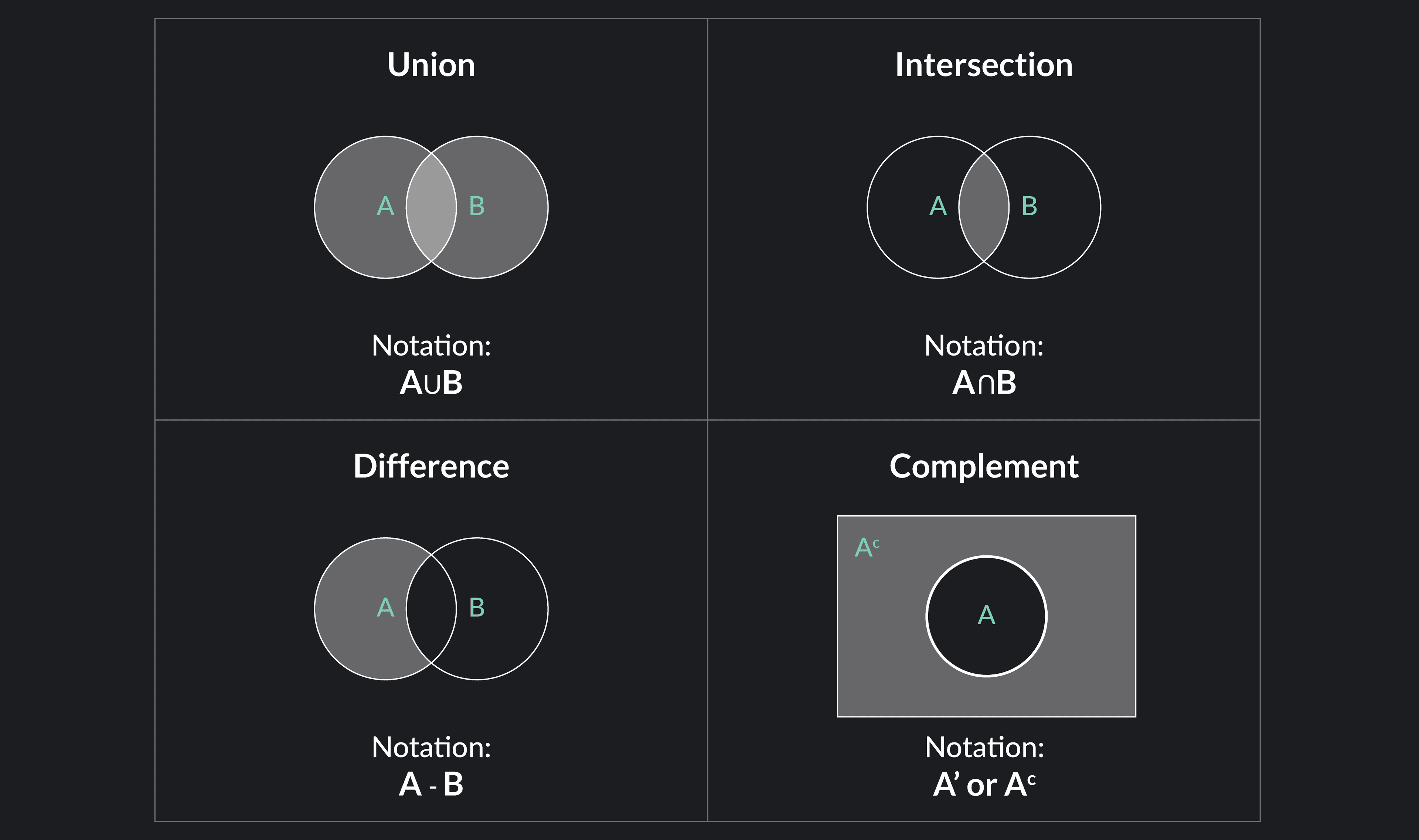
We often represent set operations using Venn Diagrams. In a Venn Diagram, a circle represents each set. The relationship between sets is visually conveyed by the extent to which each circle overlaps with the other. The overlapping sections represent elements that exist in both sets.
4 Set Operations
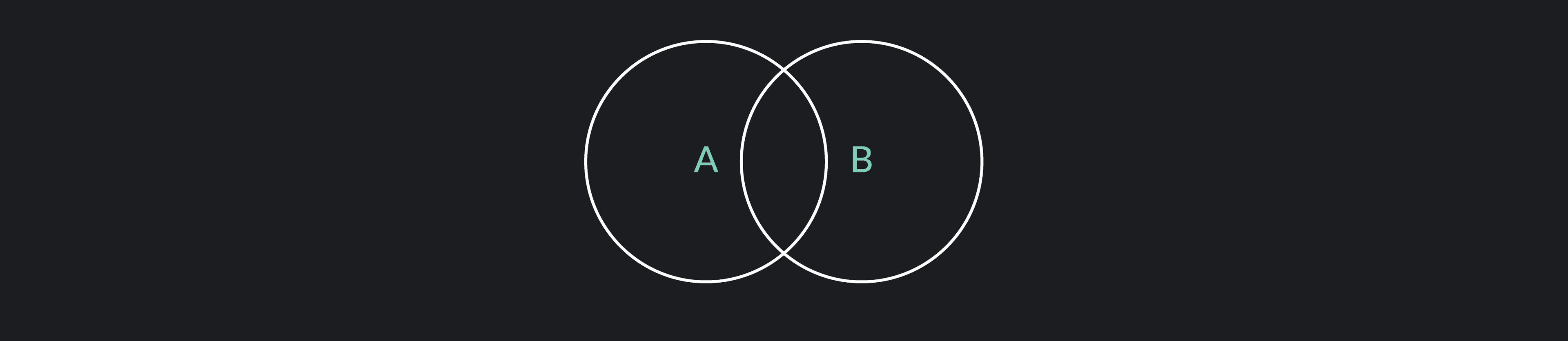
Using Venn diagrams, let’s inspect each of the main set operations.
1. Union (A∪B)
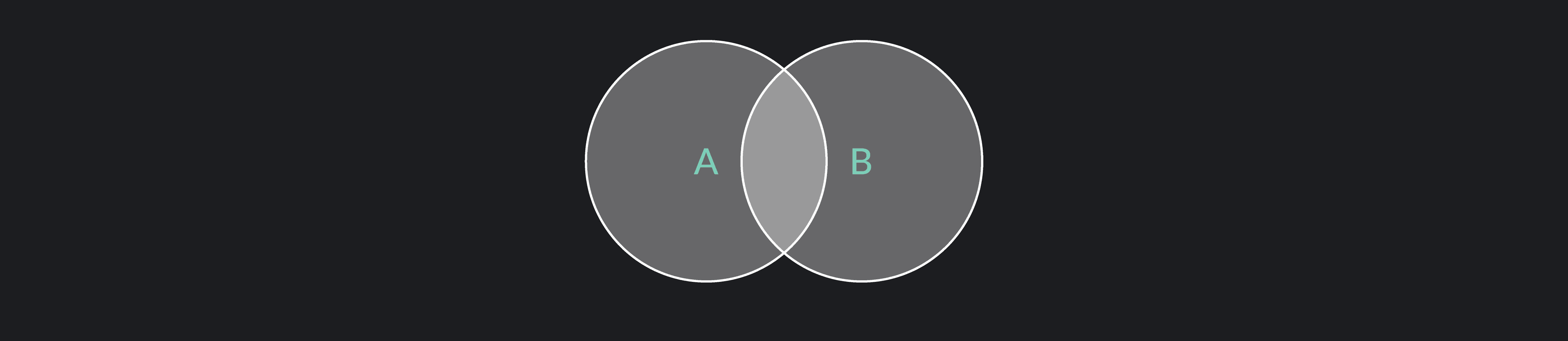
The union of two sets, A and B, is the set of distinct elements that are in Set A, Set B, or both A and B.
In a Venn diagram, the union of Set A and Set B is represented by the area distinct to Set A, plus the area distinct to Set B, plus the overlapping portion belonging to both sets.
Example:
If A = {1, 2, 3, 4, 5} and B = {3, 4, 5, 6}, the union of Set A and Set B, A∪B = {1, 2, 3, 4, 5, 6}.
2. Intersection (A∩B)
The intersection of two sets, A and B, is the set of elements that are in BOTH Set A and Set B. In a Venn diagram, the intersection is the part where the two sets overlap.
Example:
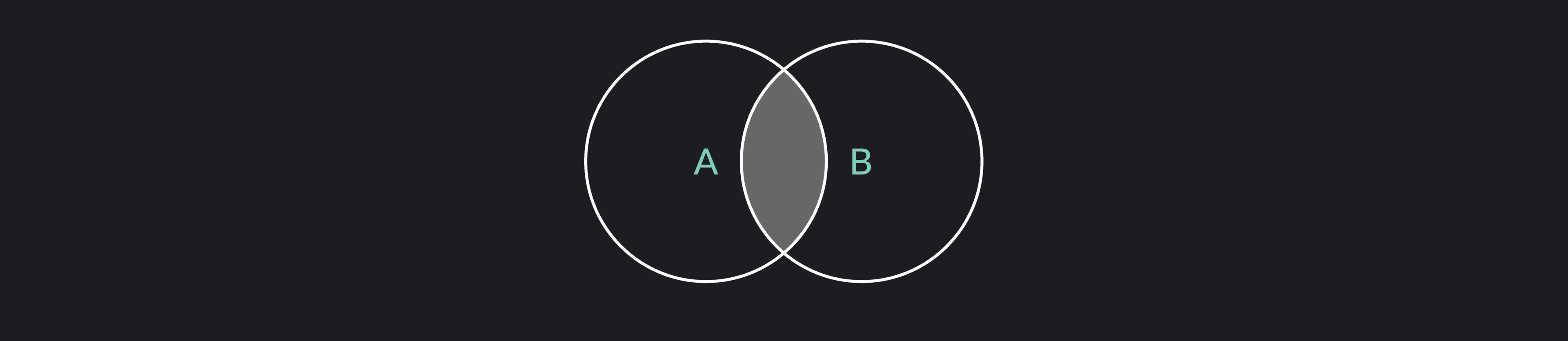
If A = {2, 4, 6, 8, 10} and B = {3, 6, 9, 12, 15}, the intersection of Set A and Set B, A∩B = {6}.
3. Difference (A-B)
The difference of two sets, A-B, is the set of elements that are unique to Set A. In other words, the difference includes the elements that are only in Set A and are not in Set B.
In a Venn diagram, the difference of A and B is the area of circle A minus the part where the two sets overlap.
Example:
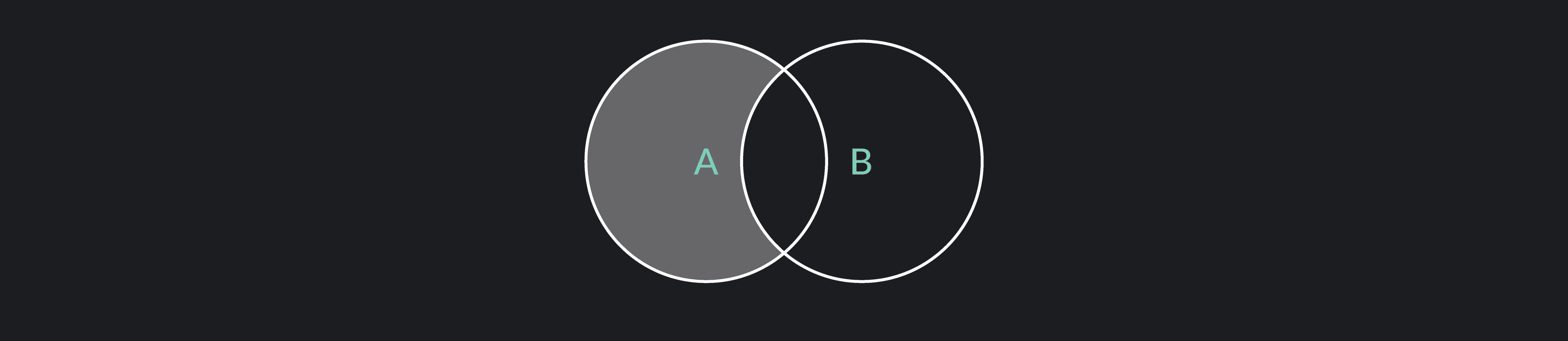
If A = {4, 8, 12, 16, 20} and B = {4, 5, 16, 18, 20 }, the difference of Set A and Set B, A-B = {8, 12}.
4. Complement
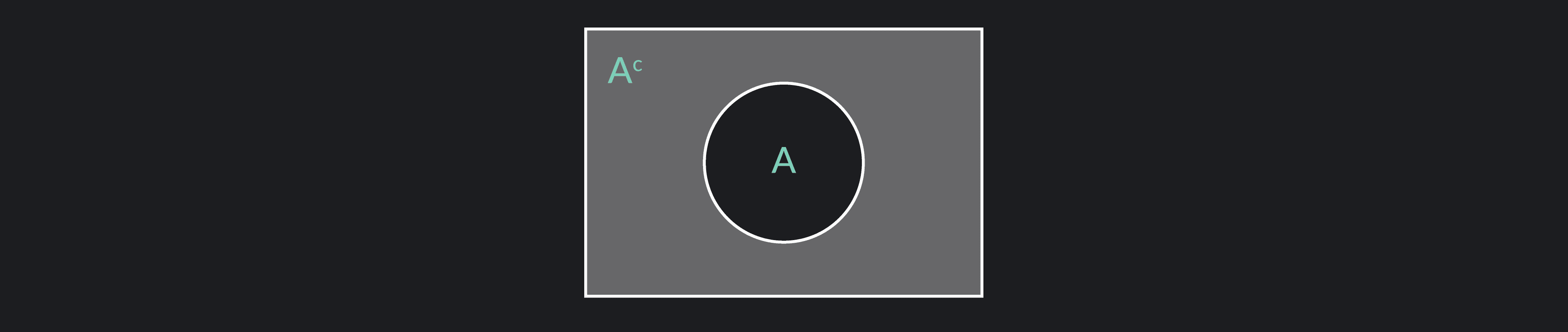
The complement of a set is often denoted by A’ (or ).
The complement of a set, Set A, are the elements in a given universal set, Set U, that are not in Set A. A universal set is a set containing all given objects.
Properties of Set Operations
Just as basic math operations (+, -,÷,×) have specific properties, set operations also have distinct properties. Here are some of them.
1. Commutative Law
The commutative law for sets is similar to the commutative property of basic mathematical operations, such as addition and multiplication. Just as 3+4 is equal to 4+3, the union (or intersection) of Set A and Set B is equal to the union (or intersection) of Set B and Set A.
2. Associative Law
The associative law for sets is similar to the associative property for basic mathematical operations. Just as 3+(4+5) = (3+4)+5, the associative law for set operations states that when finding the union or intersections of three sets, the grouping (or association) between the sets does not affect the result.
The union between Sets A, B, and C is not affected by the grouping (or association) of the sets.
The intersection between Sets A, B, and C is not affected by the grouping (or association) of the sets.
3. Distributive Law
The distributive law for unions states that the union between Set A and the intersection of Sets B and C is equal to the intersection of the union of Set A and B and the union of Sets A and C.
The distributive law for intersections states that the intersection between Set A and the union of Sets B and C is equal to the union between the intersection of Sets A and B and the intersection of Sets A and C.
This is similar to the distributive law for multiplication, which states, for example, that 2(3+4) = (2x3)+(2x4).
4. DeMorgan’s Law
DeMorgan’s law has two parts. The first states that the complement of the union of two sets, A and B, is equal to the intersection of the complement of A and the complement of B. The second part states that the complement of the intersection of two sets, A and B, is equal to the union of the complement of A and the complement of B
= |
= |
5. Idempotent Property
The idempotent property states that the union of a set with itself is just equal to the set. Similarly, the intersection between a set and itself is equal to the set.
Additional Terms for Set Theory and Set Operations
Here are some other key terms you may come across when studying set theory and set operations:
Empty Set - An empty set is a set that has no elements.
Singleton - A singleton (or a unit set) contains just one element.
Finite Set - A finite set is a set with a countable number of elements.
Infinite Set - An infinite set is a set with an unlimited number of elements.
Common Elements - Common elements are elements that are common to both sets. These are the elements in the intersection of the sets.
Subsets - A set, A, is a subset of another set, B, if all of the elements in A are also in B.
Disjoint Sets - Two sets, A and B, are said to be disjoint if they have no elements in common.
Symmetric Difference - The symmetric difference of two sets, A and B, is the set of all elements in A or B, but not in the intersection of A and B.
Practice Set Operations
Test your understanding of set operations with these five exercises. You can check your answers at the end.
Exercise 1
Find the union between Set A and Set B, A ∪ B.
A = {blue, purple, orange, yellow, gray}
B= {blue, green, pink, black}
Exercise 2
Find the intersection between Set A and Set B, A ∩ B.
A = {25, 30, 35, 40}
B= {23, 24, 25, 26, 27, 28, 29, 30}
Exercise 3
Find the difference of Set A and B, A-B.
A = {-1, 0, 3, 5}
B= {1, 2, 3, 4, 7, 12}
Exercise 4
Find the complement of Set A, .
U = {Skittles, Kit Kat, Snickers, Starbursts, Smarties, Warheads, Reese’s}
A = {Kit Kat, Snickers, Reese’s}
Exercise 5
Match each set property to its appropriate equation.
Associative Law of Intersections ____
Commutative Law of Unions ____
Distributive Law of Intersection ____
DeMorgan’s Law of Unions ____
Idempotent Property for Intersections ____
a. A ∪ (B ∪ C) = (A ∪ B) ∪ C
b. A ∩ B = B ∩ A
c. A ∩ (B ∩ C) = (A ∩ B) ∩ C
d. A ∪ B = B ∪ A
e. A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
f. A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
g. =
h. =
i. A ∪ A = A
j. A ∩ A = A
Solutions:
A ∪ B = {blue, purple, orange, yellow, gray, green, pink, black}
A ∩ B = {25, 30}
A - B= {-1, 0, 5}
= {Skittles, Starbursts, Smarties, Warheads}
C, D, F, G, J
Explore Outlier's Award-Winning For-Credit Courses
Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.
Check out these related courses:
Related Articles
Statistics
What Do Subsets Mean in Statistics?
This article explains what subsets are in statistics and why they are important. You’ll learn about different types of subsets with formulas and examples for each.
Sarah Thomas
Subject Matter Expert
Statistics
How To Calculate Variance In 4 Simple Steps
The article explains what variance means, how to calculate it, how to use the formula and the main differences between variance and standard deviation.
Sarah Thomas
Subject Matter Expert