How To Find Relative Extrema [Calculus 101]

In This Article

1. What Are Relative Extrema?

2. How To Find Relative Extrema

3. The First Derivative Test and Critical Points

4. 3 Examples of Finding Relative Extrema

What Are Relative Extrema?

Relative extrema are the points on a function where the curve changes direction from increasing to decreasing, or from decreasing to increasing. On a graph, these points look like peaks and valleys. These are the points on a function where the derivative changes from positive to negative, or from negative to positive.

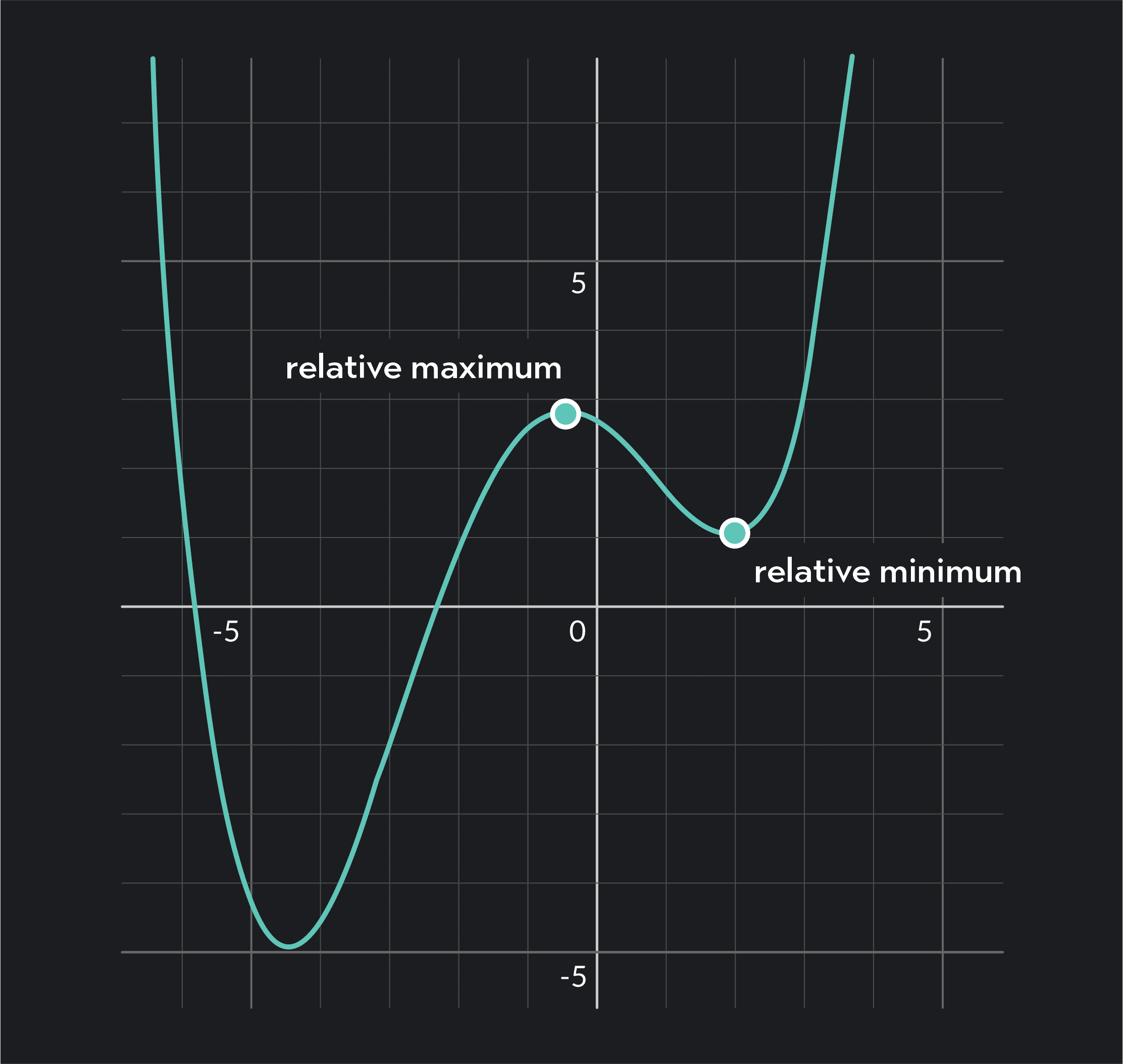
For instance, let’s say $y = f(x)$ has a relative maximum at $x = a$. Then for all x-values of the function close to $a$, $f(x)$ is less than or equal to $f(a)$.

On the other hand, let’s say $f(x)$ has a relative minimum at $x = b$. Then for all x-values of the function close to $b$, $f(x)$ is greater than or equal to $f(b)$.

Relative maxima and relative minima are types of local extrema. An absolute maximum and absolute minimum, by contrast, are the very highest and lowest points on the curve over the entire domain of the function.

Note that relative maxima and minima are y-values; this means that the maximum values and minimum values are equal to the height of the curve $f(c)$ at some point $c$.

How To Find Relative Extrema

Here are the definitions of relative maxima and minima:

• At a relative minimum, the slope of the function is zero or undefined, and the function changes from decreasing to increasing.

• At a relative maximum, the slope of the function is zero or undefined, and the function changes from increasing to decreasing.

You can use several effective methods to find the relative extrema of a function. These include the Second Derivative Test, the First Derivative Test, and examining the graph of the function. Derivative tests explain how a function’s derivative changes its shape. Here’s an in-depth explanation: The Second Derivative Test is often the fastest of the three methods.

Here are the steps to using the Second Derivative Test to find relative extrema:

1. Take the first derivative of the function.

2. Find the critical points of the function where the first derivative is zero. The critical points $c$ where $f’(c) = 0$ are also called stationary points. To find the stationary points, set the first derivative equal to zero and solve for $x$.

3. Take the second derivative of the function. To do this, take the derivative of the first derivative.

4. For each stationary point $x$, plug $x$ into the second derivative function, and interpret the results.

• If $f"(x)$ is positive, then the function has a relative minimum at $x$.

• If $f"(x)$ is negative, then the function has a relative maximum at $x$.

• If $f"(x)$ is zero or non-existent at $x$, then the test is inconclusive.

When the Second Derivative Test fails, other methods must be used to determine if ‌local extrema is at the critical point, such as the First Derivative Test.

The First Derivative Test and Critical Points

In calculus, a critical point is a point on a function where the derivative of the function is either zero or undefined. All local extrema occur at critical points, but not all critical points are local extrema.

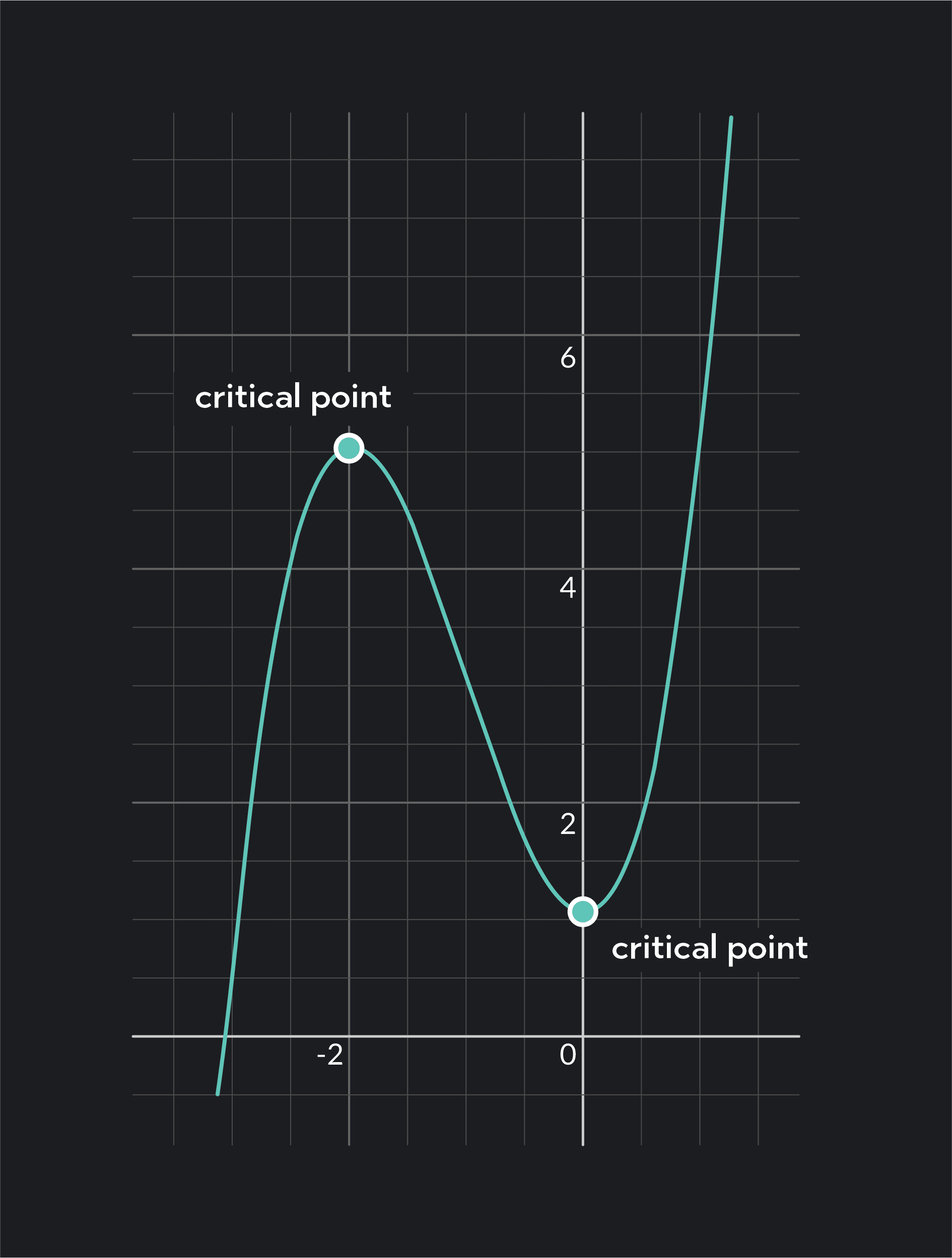
The First Derivative Test is one method for determining whether a critical point corresponds to a local maximum, local minimum, or neither. The test involves analyzing the sign of the first derivative of the function on either side of the critical point.

If the function changes direction (from increasing to decreasing or decreasing to increasing) at the critical point, then that point is a relative minimum or relative maximum.

Here are the steps to using the first derivative test:

1. Take the first derivative of the function.

2. Find the critical numbers of the function by setting the first derivative equal to zero. Also identify the points where the function is undefined.

3. Determine whether the critical value corresponds to a relative maximum, relative minimum, or neither by analyzing the sign of the first derivative on either side of the critical point. We can do this by using test points.

• If the function is increasing on the left and decreasing on the right of the critical point, then the critical point is a relative maximum.

• If the function is decreasing on the left and increasing on the right of the critical point, then the critical point is a relative minimum.

When thinking about relative extrema, it's important to understand the concept of increasing and decreasing intervals. Relative extrema occur at the points where a curve changes from increasing to decreasing, and vice versa.

Suppose a function $f$ is differentiable on the interval $I$. Then:

• If $f’(x) > 0$ for each $x$ on $I$, then $f$ is increasing on $I$.

• If f’(x) < 0 for each x on I, then f is decreasing on I.

• If $f’(x) = 0$ for each $x$ on $I$, then $f$ is constant on $I$.

3 Examples of Finding Relative Extrema

Relative extrema play a crucial role in many applications of calculus, including optimization problems in economics, physics, and engineering. Let’s practice with some relative extrema calculus problems.

We’ll use the Second Derivative Test, the First Derivative Test, and practice finding relative extrema on a graph.

Example 1

Consider the function $f(x) = x^2 - 12x + 36$. Find its relative extrema.

We can find the critical points by setting the first derivative equal to zero:

Setting $f'(x) = 0$, we get $x = 6$. We can use the Second Derivative Test to determine the nature of this critical point. Taking the second derivative, we have:

Evaluating $f''(x)$ at $x = 6$, we get $f''(6) = 2$. Since $f''(6)$ is positive, the function has a relative minimum at $x = 6$ of $f(6) = 0$.

Example 2

Consider the function $g(x) = x^3 + 3x^2 - 24x + 2$. Find its relative extrema.

We can find the critical points by setting the first derivative equal to zero:

Setting $g'(x) = 0$, we get $3(x+4)(x-2) = 0$. Solving for $x$, we get $x = 2$ and $x = -4$. These are our two critical points. We can use the First Derivative Test to determine the nature of these critical points:

• By plugging test points to the left of $x = 2$ into the first derivative, we find that the derivative is negative. Therefore, the function is decreasing to the left of $x = 2$. By plugging test points to the right of $x = 2$ into the first derivative, we find that the derivative is positive. Therefore, the function is increasing to the right of $x = 2$. Thus, a relative minimum is at $x = 2$ of $g(2) = -26$.

• By plugging test points to the left of $x = -4$ into the first derivative, we find ‌the derivative is positive. Therefore, the function is increasing to the left of $x = -4$. By plugging test points to the right of $x = -4$ into the first derivative, we find ‌the derivative is negative. Therefore, the function is decreasing on the right of $x = -4$. Therefore, a relative maximum is at $x = -4$ of $g(-4) = 82$.

Example 3

Consider the function $h(x) = 6x^{\frac{2}{3}} - 4x$.

We will find the relative extrema by analyzing the graph of the function:

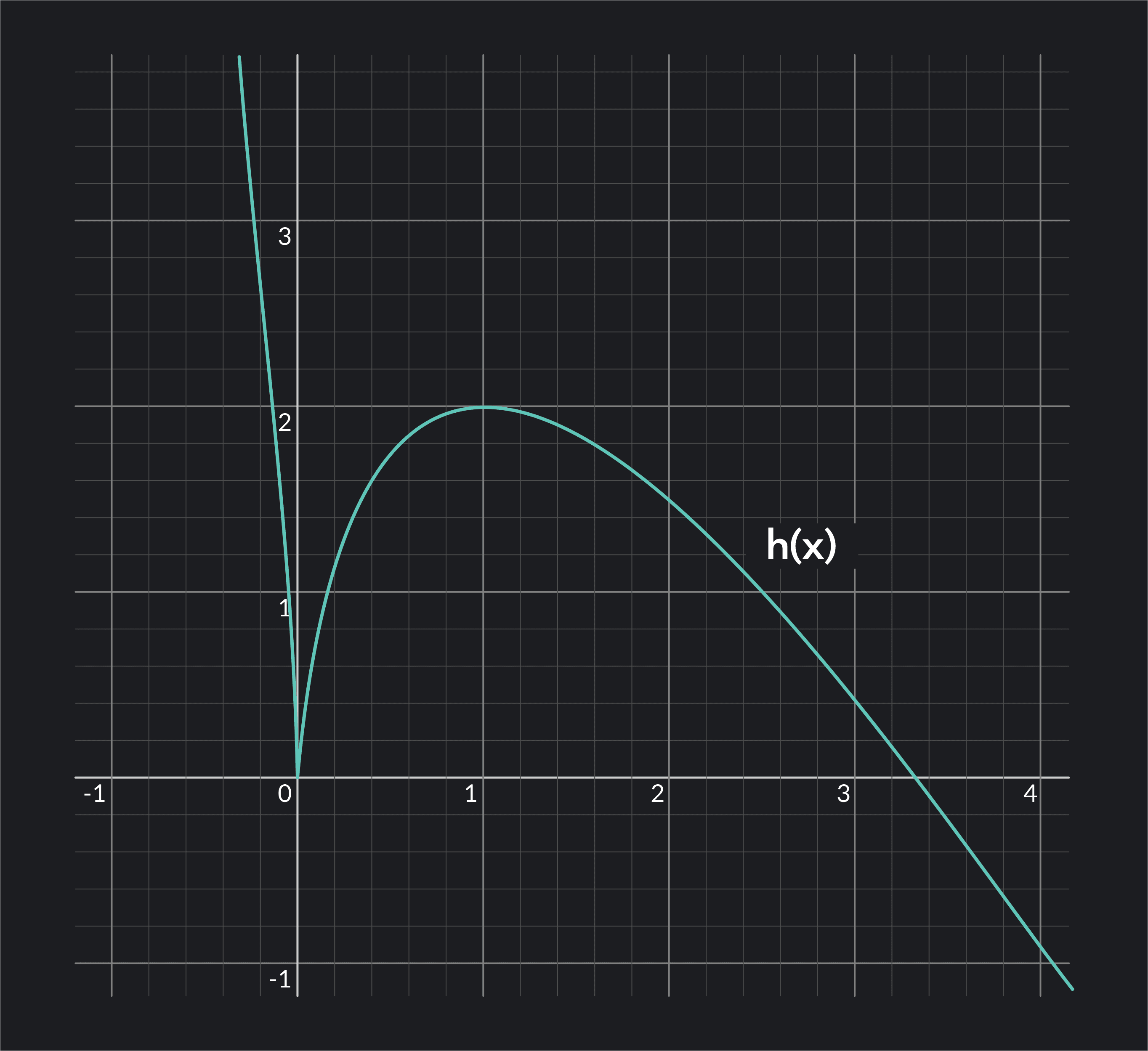
From the graph of $h(x)$, we can see ‌the function has a relative minimum of 0 at $x = 0$, and a relative maximum of 2 at $x = 1$. At $x = 0$, the direction of the function changes from decreasing to increasing, and at $x = 1$, the direction of the function changes from increasing to decreasing.

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Calculus I

The mathematics of change.

Explore course

Calculus I

The mathematics of change.

Explore course

Intro to Statistics

How data describes our world.

Explore course

Intro to Statistics

How data describes our world.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course