Understanding the Squeeze Theorem

In This Article

1. What Is the Squeeze Theorem?

2. Squeeze Theorem Proof

3. Step-By-Step Guide to the Squeeze Theorem

4. Squeeze Theorem Examples

5. 5 Tips When Using the Squeeze Theorem

What Is the Squeeze Theorem?

The Squeeze Theorem is a method for evaluating the limit of a function. Also known as the Sandwich Theorem, the Squeeze Theorem traps one tricky function whose limit is hard to evaluate, between two different functions whose limits are easier to evaluate.

To introduce the logic behind this theorem, let’s recall a familiar algebraic property. This rule is similar in logic to the transitive property of equality in algebra. For example, if $a \leq b \leq c$ and $a = c$, then $b$ also equals $c$.

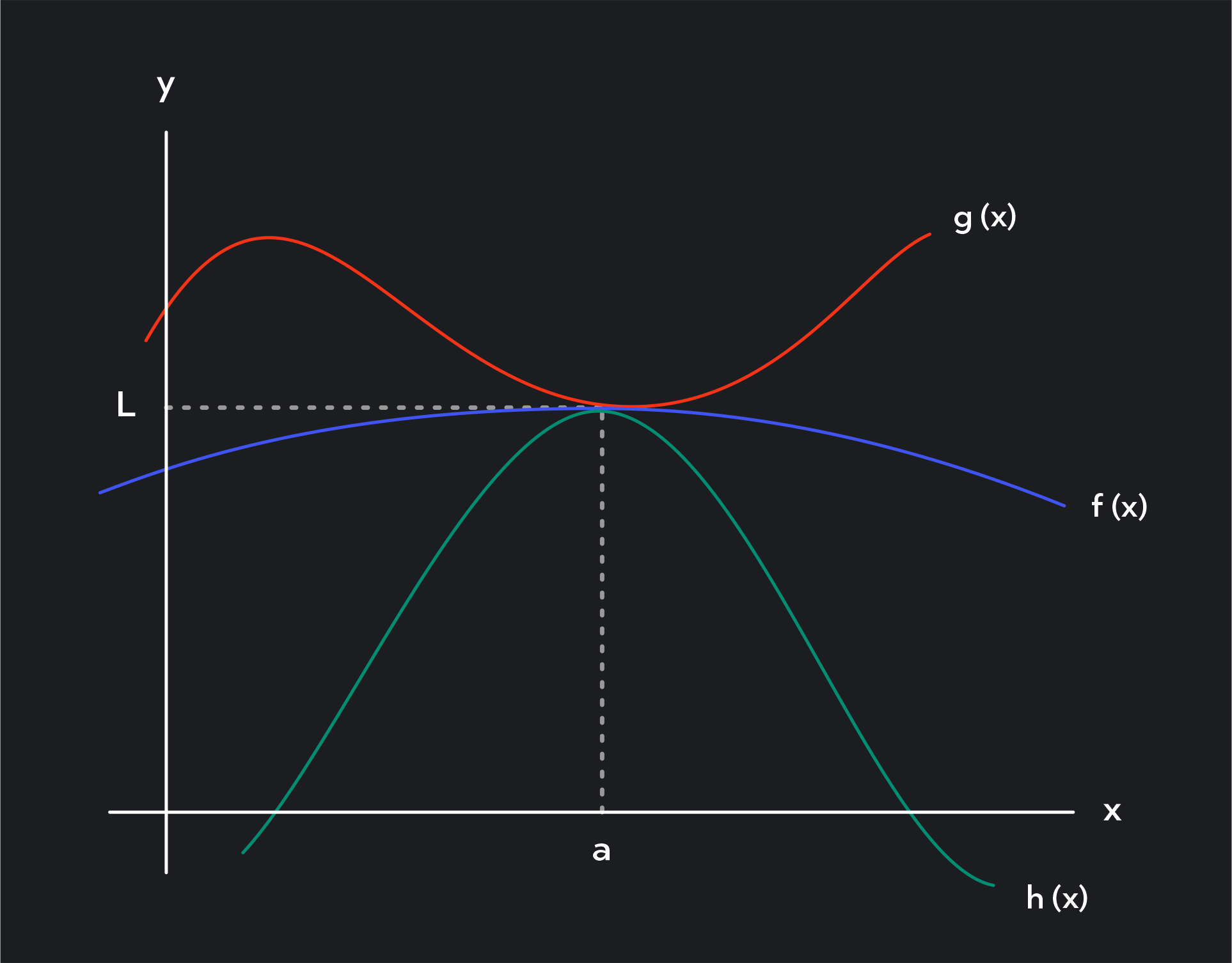
In the same vein of thought, if $g(x) \leq f(x) \leq h(x)$ for all $x$ on some open interval containing $c$, and $\lim_{x\to c}g(x) = \lim_{x\to c}h(x) = L$, then $\lim_{x\to c}f(x) = L$. This is the Squeeze Theorem definition.

The following figure provides a graphical proof of the Squeeze Theorem. Do you see how “squeezing” or “sandwiching” a hard function between two easier functions allows us to find its limit?

Squeeze Theorem Proof

If graphical proofs aren’t your jam, we can also prove the Squeeze Theorem using the epsilon-delta ($\epsilon - \delta$) definition of limits. The $\epsilon - \delta$ definition goes like this:

Let the function f(x) be defined on an open interval, and let c be on this interval. Then \lim_{x\to c}f(x) = L if for all \epsilon > 0, there exists some \delta > 0 such that when 0 < |x - c | < \delta, then this immediately implies that |f(x) - L| < \epsilon.

To begin our proof, let’s start with our assumptions: $g(x) \leq f(x) \leq h(x)$ for all $x$ on some open interval containing $c$, and $\lim_{x\to c}g(x) = \lim_{x\to c}h(x) = L$. We want to prove that $\lim_{x\to c}f(x) = L$ using the above definition.

Using this definition, our second assumption tells us that for all \epsilon > 0, there exists \delta_1 > 0 such that when 0 < |x - c | < \delta_1, then |g(x) - L| < \epsilon. Similarly, for all \epsilon > 0, there exists \delta_2 > 0 such that when 0 < |x - c | < \delta_2, then |h(x) - L| < \epsilon.

We’ll let \delta = \min \{\delta_1, \delta_2\}. This implies that when 0 < |x - c | < \delta, then |g(x) - L| < \epsilon and |h(x) - L| < \epsilon. We can rewrite this to say -\epsilon < g(x) - L< \epsilon and -\epsilon < h(x) - L < \epsilon. Adding L to each side, if 0 < |x - c | < \delta, then L -\epsilon < g(x) < L + \epsilon and L -\epsilon < h(x) < L + \epsilon.

Applying these new inequalities to our first assumption, we get L - \epsilon < g(x) \leq f(x) \leq h(x) < L + \epsilon, which implies that L - \epsilon < f(x) < L + \epsilon. Subtracting L from each side, we get - \epsilon < f(x) - L < \epsilon. We can rewrite this as |f(x) - L| < \epsilon.

This concludes our proof. Thus, $\lim_{x\to c}f(x) = L$.

Step-By-Step Guide to the Squeeze Theorem

How do you use the squeeze theorem? Well, if $f(x)$ is sandwiched between two functions $g(x)$ and $h(x)$ near $c$, and if $g(x)$ and $h(x)$ have the same limit $L$ at $c$, then $f(x)$ is trapped between them and must also have the same limit $L$ at $c$!

Here are 4 simple steps to using the Squeeze Theorem:

1. Use equalities to find two functions $g(x)$ and $h(x)$.

2. Show that $f(x)$ lies between $g(x)$ and $h(x)$ near $c$.

3. Show that $\lim_{x\to c}g(x) = L$.

4. Show that $\lim_{x\to c}h(x) = L$.

Squeeze Theorem Examples

We’ll walk through a few examples of the squeeze theorem together.

1. Use the Squeeze Theorem To Evaluate

Use the Squeeze Theorem to evaluate $\lim_{x\to0}f(x)$ where $f(x) = x^2\cos(\frac{1}{x^2})$.

How can we sandwich $f(x)$ between two other functions? Let’s use equalities. For now, we’ll just focus on $\cos{(\frac{1}{x^2})}$. The fraction might look daunting, but since this is an oscillating cosine function, we know the following statement is true:

Multiply all sides by $x^2$ to get our original function in the middle.

This gives us:

This equality gives us two functions ‌we can use, $g(x) = -x^2$ and $h(x) = x^2$. Our next step is to take the limit of $g(x)$ and $h(x)$ as $x$ approaches 0, and see if their limits match:

Their limits match! We’ve now shown $f(x)$ is squeezed between $g(x)$ and $h(x)$, and $\lim_{x\to 0 }g(x) = \lim_{x\to 0 }h(x) = 0$.

By the Squeeze Theorem, we can conclude:

Our answer is $\lim_{x\to 0 }f(x) = 0$.

2. Use the Squeeze Theorem To Compute

Use the Squeeze Theorem to compute $lim_{x\to0}f(x)$ where $f(x) = x \sin{(\frac{1}{x})}$.

We want to pinch f(x) between two functions whose limits are more easily evaluated at x = 0. Let’s break this down. We’ll ignore x for now, and just focus on \sin{(\frac{1}{x})}.

Since this is a sine function, we know that:

We have to be careful here. We can’t multiply both sides by $x$, since $x$ can be negative and our inequality will be thrown off.

We’ll rewrite our expression using absolute value instead:

Now, we’ll multiply both sides of our equation by $|x|$:

We now have two functions ‌we can use, $g(x) = 0$ and $h(x) = |x|$. Let’s take the limit of $g(x)$ and $h(x)$ as $x$ approaches 0, and see if these limits match:

The limits match! We’ve shown that g(x) < |f(x)| < h(x) and \lim_{x\to 0 }g(x) = \lim_{x\to 0 }h(x) = 0.

By the Squeeze Theorem, we can conclude:

Therefore, $\lim_{x\to 0 }|x \sin{(\frac{1}{x})}| = 0$. Since this answer is 0, this immediately implies that $\lim_{x\to 0 }x \sin{(\frac{1}{x})} = 0$.

5 Tips When Using the Squeeze Theorem

Here are a few additional tips to consider when using the Squeeze Theorem.

1. What functions is this pinching theorem most ‌used for? This method is especially useful for oscillating sine and cosine functions, as well as other trigonometric functions.

2. We use the Squeeze Theorem when other methods don’t work, such as factoring, trigonometry substitutions, rationalization, or other algebraic manipulations.

3. It is a good idea to be familiar with radians and the unit circle. Many Squeeze Theorem problems will use trig functions.

4. When in doubt, graph it! Is $f(x)$ sandwiched between $g(x)$ and $h(x)$ on the necessary interval? Do their limits look the same at the right particular point? Graphing can help validate your answer.

5. Remember, the limits of your lower and upper bounds must match. Otherwise the theorem can’t be used.

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Calculus I

The mathematics of change.

Explore course

Calculus I

The mathematics of change.

Explore course

Intro to Statistics

How data describes our world.

Explore course

Intro to Statistics

How data describes our world.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course