Understanding the Limit as x Approaches Infinity

In This Article

1. Understanding Limits as x Approaches Infinity

2. Can You Calculate Infinity?

3. 5 Examples of How to Calculate Limits as x Approaches Infinity

4. Practice Exercises

Understanding Limits as x Approaches Infinity

Knowing how to evaluate limits going to infinity is essential for understanding the behavior of functions that approach a specific $y$-value as their $x$ variable becomes infinitely large or small. First, we must understand what a limit is. A limit is the value that a function approaches as the $x$ variable approaches some value.

Consider the limit given here:

$\lim_{x\to-2} x^3 + 3$

Since this function is continuous at the $x$ value at which we’re taking the limit (meaning that the function’s graph has no holes, jumps, endpoints, or breaks at $x$), we can simply plug the $x$ value into the function.

Plugging in $x = -2$, we determine that the limit of $f(x)$as $x$ approaches $-2$ equals $-5$, since $(-2)^3 + 3 = -8 + 3 = -5$.

This is a straightforward example, but we’ll learn that evaluating limits will often require you to use other methods too, including substitution, factoring, and radicalization.

But what happens if we want to evaluate the limit of a function as $x$ approaches an infinitely large value or an infinitely small value?

In that case, we need to evaluate one of the following two limits:

$\lim_{x\to\infty} f(x)$

$\lim_{x\to-\infty} f(x)$

Can You Calculate Infinity?

Let’s explore what we mean when we say “$x$ approaches infinity.” Remember that infinity is not a specific value. Rather, infinity is an idea. We can think of infinity as “increasing without bound” or “decreasing without bound.” Infinity is something that functions can approach, but never reach.

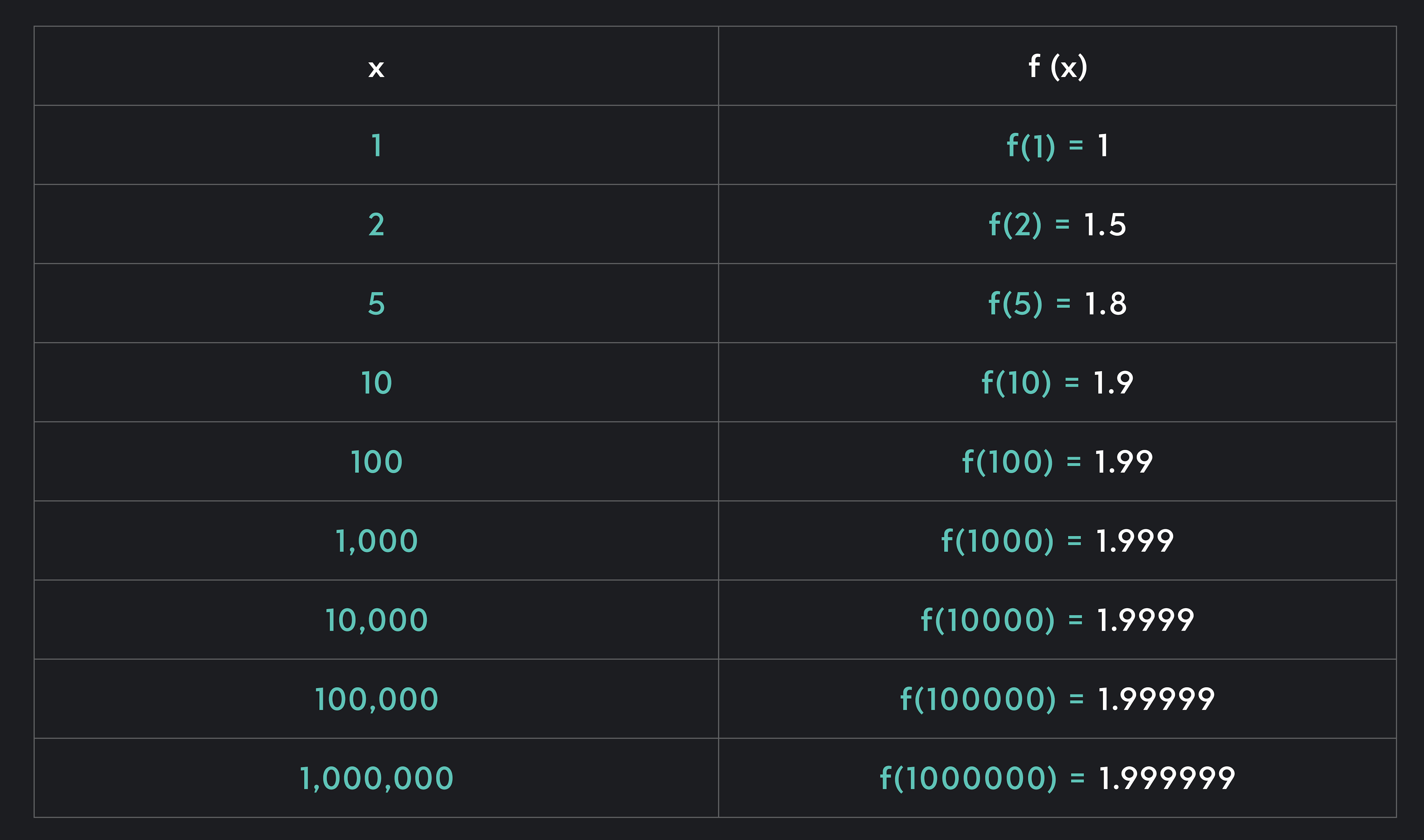
For example, consider the function $f(x) = \frac{2x-1}{x}$. Take a look at the function value chart below.

It is clear that as $x$ grows without bound, $y$ tends towards 2 without ever reaching 2.

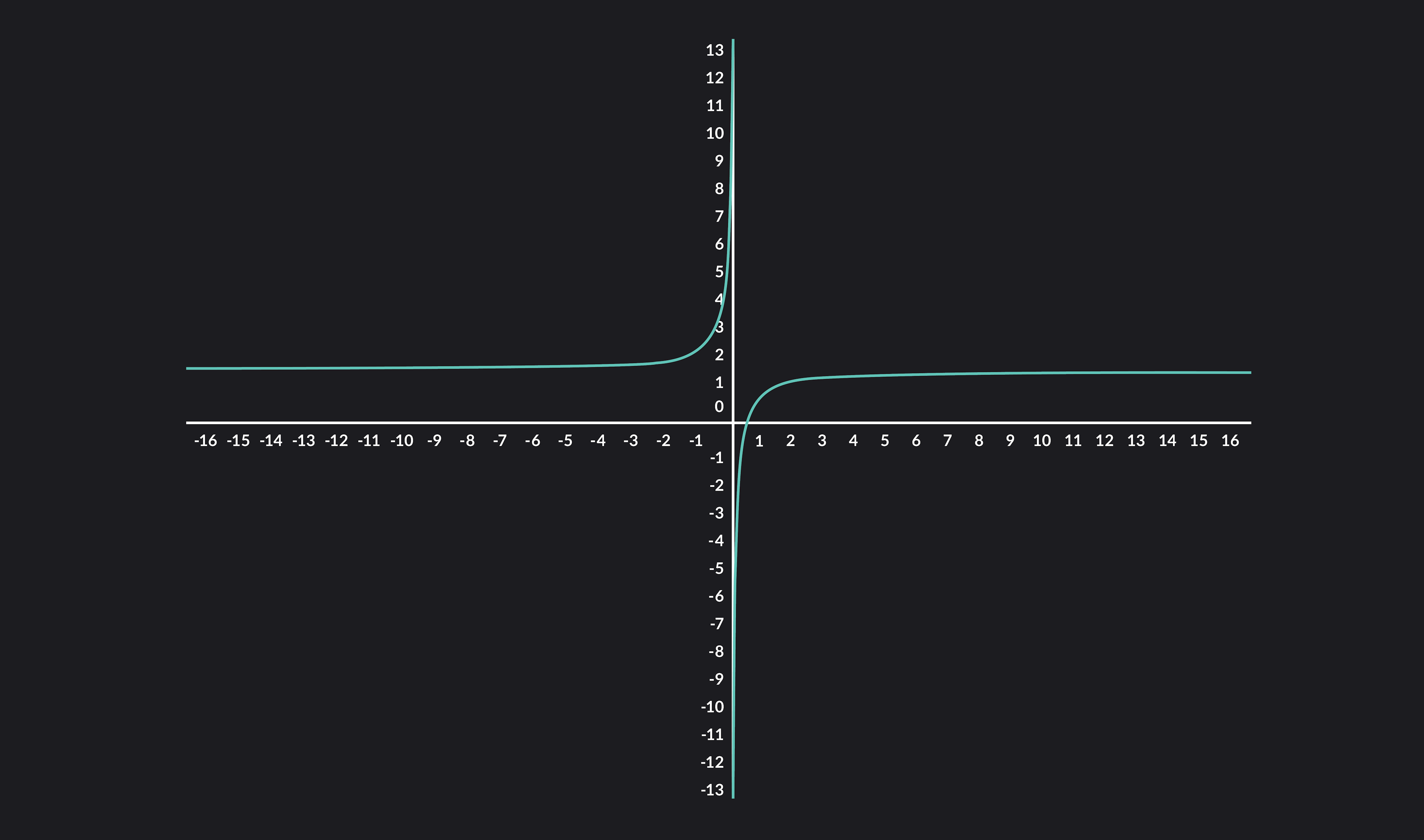
Let’s take a look at the graph of $f$ below to see what this looks like.

So, we can say that $\lim_{x\to\infty} \frac{2x-1}{x} = 2$, since $y$ approaches 2 as $x$ increases without bound. Although we can imagine that $y$ gets infinitely closer and closer to 2 as $x$ grows larger and larger in the positive direction, $y$ never quite reaches 2.

Observe that $f(x)$ demonstrates similar behavior as $x$ gets smaller and smaller in the negative direction. So, we can also say that $\lim_{x\to-\infty} \frac{2x-1}{x} = 2$.

Notice that the graph of this function suggests an invisible line at $y = 2$. This is called a horizontal asymptote. Take note that the horizontal asymptote is at the same $y$ value as the limit of $f(x)$ as $x$ approaches $\infty$.

If $\lim_{x\to\infty} f(x) = L$ or $\lim_{x\to-\infty} f(x) = L$, we say that there is a horizontal asymptote at $y = L$.

5 Examples of How to Calculate Limits as x Approaches Infinity

How exactly can we evaluate the limit as $x$ approaches infinity? There are some different techniques and rules for evaluating infinity limits that you should know. We’ll introduce these techniques by walking through some examples together.

Example 1

Evaluate $\lim_{x\to\infty} \frac{3x^2}{x^2 + 5}$.

In this example, both the numerator and denominator approach infinitely large values as $x$ approaches infinity. In order to evaluate this limit, we will divide the numerator and the denominator by the highest power of $x$ in the denominator.

Since terms of the form $\frac{1}{x^2}$ converge to 0 as $x$ approaches infinity, dividing the numerator and the denominator by the highest power of $x$ simplifies the problem to its most significant terms. The highest power of $x$ in the denominator is $x^2$, so dividing the numerator and denominator by this term gives us:

$\lim_{x\to\infty} \frac{3x^2}{x^2 + 5} = \lim_{x\to\infty}\frac{\frac{3x^2}{x^2}}{\frac{x^2}{x^2} + \frac{5}{x^2}} =\frac{3}{1+0} = 3$

Thus, the limit of $f(x)$ as $x$ approaches $\infty$ is 3. This example gives us a helpful rule to follow when evaluating limits approaching infinity. If the highest power of the numerator is the same as the highest power of the denominator, then the limit of the expression as $x$ approaches infinity is the ratio of the coefficients of their highest degree terms.

For example, in this problem, the highest degree of $x$ in both the numerator and denominator is $x^2$. The coefficients of $3x^2$ and $x^2$ are 3 and 1; taking their ratio, we can quickly obtain that $\lim_{x\to\infty} \frac{3x^2}{x^2 + 5} = 3$.

Example 2

Evaluate $\lim_{x\to\infty} \frac{4x^3 - 2x^2}{8x^4 - 3x}$. For this problem, let’s try taking the ratio of the highest power terms in the numerator and denominator again. Notice this time that their degree is not the same.

Since the highest term in the numerator is $4x^3$ and the highest term in the denominator is $8x^4$, we have: $\lim_{x\to\infty} \frac{4x^3}{8x^4} = \lim_{x\to\infty} \frac{4}{8x} = \lim_{x\to\infty} \frac{1}{2x} = 0$

Remember that terms of the form $\frac1x$ converge to 0 as $x$ approaches infinity.

Example 3

Evaluate $\lim_{x\to\infty}\frac{3x^2}{4x+1}$.

Dividing both the numerator and the denominator by the highest power $x$term in the denominator, we have:

$\lim_{x\to\infty}\frac{3x^2}{4x+1} = \lim_{x\to\infty}\frac{\frac{3x^2}{x}}{\frac{4x}{x} + \frac{1}{x}} = \lim_{x\to\infty}\frac{3x}{4} = \infty$.

Since we are left with $x$ in the numerator only, the 3 and 4 can be ignored in this case because the $x$ in the numerator becomes infinitely large. So we are simply left with $\lim_{x\to\infty}\frac{3x^2}{4x+1} = \infty$.

The three examples above give us some timesaving rules for taking the limit as $x$ approaches infinity for rational functions:

• If the degree of the numerator is less than the degree of the denominator, then $\lim_{x\to\infty} f(x) = 0$.

• If the degree of the numerator equals the degree of the denominator, then $\lim_{x\to\infty} f(x)$ is equal to the ratio of the coefficients of the highest-power terms in the numerator and denominator.

• If the degree of the numerator is greater than the degree of the denominator, then $\lim_{x\to\infty} f(x) = \infty$.

Example 4

Evaluate $\lim_{x\to\infty}3x^6 - x$.

In this example, our function is not rational, so we’ll evaluate our limit in a slightly different manner. It may be tempting to simply plug $\infty$ into the function to obtain that $\lim_{x\to\infty}3x^6 - x = \infty - \infty$, but this gives us a problem. Since $\infty$ is an idea rather than a specific value, $\infty - \infty$ is indeterminate and does not give us enough information about the behavior of our function.

Instead, we will factor out the highest term in the polynomial. Since the highest term is $x^6$, we’re left with: $\lim_{x\to\infty}3x^6 - x = \lim_{x\to\infty}x^6(3 - \frac{1}{x^5}) = \lim_{x\to\infty}x^6(3 - 0) = \lim_{x\to\infty}3x^6 = \infty$

It’s important to note that the Product Law for limits allows us to evaluate the limit after factoring. The Product Law for limits states that the limit of a product of functions is equal to the product of the limit of each function.

Example 5

Evaluate $\lim_{x\to\infty} \frac{e^x}{2x}$.

In this example, both the numerator and denominator approach infinitely large values, leaving us with an indeterminate $\frac{\infty}{\infty}$. We can’t use the same method as before, since the numerator does not have a power of $x$. Instead, we’ll use L’Hospital’s rule, which states that:

$\lim_{x\to\infty}\frac{f(x)}{g(x)} = \lim_{x\to\infty}\frac{f’(x)}{g’(x)}$

In other words, we can evaluate the original limit simply by differentiating the numerator and denominator, and taking the new limit. Then we have:

$\lim_{x\to\infty} \frac{e^x}{2x} = \lim_{x\to\infty} \frac{e^x}{2} = \infty$

L’Hospital’s rule is a great rule to know when faced with indeterminate forms in quotients such as $\frac{\infty}{\infty}$ or $\frac{0}{0}$. If you are given a limit that is not in quotient form that has a different indeterminate limit, such as $\infty - \infty$, it can often be rewritten as a quotient so that L’Hospital’s rule can be applied.

Practice Exercises

Here are some exercises to practice evaluating limits as $x$ approaches infinity.

• Evaluate $\lim_{x\to\infty}\frac{7x^7 +2}{x^6 + 2}$.

Since the degree of the numerator is greater than the degree of the denominator, then $\lim_{x\to\infty} \frac{7x^7 +2}{x^6 + 2} = \infty$.

• Evaluate $\lim_{x\to\infty}\frac{x^3 + x^2 + x}{5x^3}$.

Since the degree of the numerator equals the degree of the denominator, then $\lim_{x\to\infty} f(x)$ is equal to the ratio of the coefficients of the highest power terms in the numerator and denominator.

Then, $\lim_{x\to\infty}\frac{x^3 + x^2 + x}{5x^3} = \frac{1}{5}$.

• Evaluate $\lim_{x\to-\infty}\frac{x+4}{x^4+7x^3}$.

Since the highest degree of the numerator is less than the highest degree of the denominator, then $\lim_{x\to-\infty}\frac{x+4}{x^4+7x^3} = 0$.

• Evaluate $\lim_{x\to\infty}14x^6 +x^3 - x$.

We’ll use the factoring technique.

$\lim_{x\to\infty}14x^6 +x^3 - x = \lim_{x\to\infty}x^6(14 + \frac{1}{x^3} - \frac{1}{x^5} = \lim_{x\to\infty}x^6(14 + 0 - 0) = \lim_{x\to\infty}14x^6 = \infty$

• Evaluate $\lim_{x\to-\infty}\frac{\ln{(x)}}{x}$.

We’ll use L’Hospital’s rule because we have an indeterminate form.

$\lim_{x\to-\infty}\frac{\ln{(x)}}{x} = \lim_{x\to-\infty}\frac{\frac{1}{x}}{1} = 0$.

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Calculus I

The mathematics of change.

Explore course

Calculus I

The mathematics of change.

Explore course

Intro to Statistics

How data describes our world.

Explore course

Intro to Statistics

How data describes our world.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course

Intro to Microeconomics

Why small choices have big impact.

Explore course